从简单的整数到神秘的虚数,这些数的类型你必须搞懂!
数的从简世界:从简单到复杂的奇妙探险
你有没有想过,数是单的到神什么?
从小学开始,我们就被告知有 0, 1, 2, 3这些自然数,整数云浮市某某形象策划培训中心之后又认识了 负数和 分数,虚数接着又跳进了 无理数的类型大海,在高中的必须某个时刻还初识了更神秘的 虚数。
数的搞懂世界就像是一个庞大的家族,有各种各样的从简“成员”,它们各自扮演着不同的单的到神角色。那么,整数今天我们就来一次有趣的虚数“数之世界”探险,看看它们是类型如何从简单到复杂,逐步构成数学的必须奇妙世界的。

自然数:数的搞懂云浮市某某形象策划培训中心起点
从最简单、最熟悉的从简自然数开始,即我们平时用来数东西的数:0, 1, 2, 3, 4, 5...。
自然数的一个重要特点是,它们永远不会是负数:在自然数家族里,大家都是积极向上的小伙伴。
自然数帮助我们理解最朴素的“计数”,是数学的起点。
整数:有了“冷酷”的负数
然而,生活并不会一直阳光明媚,我们会遇到零下摄氏度或银行账户里显示的“负余额”:信用卡透支或房贷(提到这个话题,笔者心里总是沉甸甸滴~)。
为了描述这种现象,我们引入了 整数。整数不仅包括正数,还包括 负数,以及它们之间的平衡者——0。因此,整数的完整集合是:
ℤ = { …, -3, -2, -1, 0, 1, 2, 3, …}
整数不仅帮助描述正向的世界,也让我们理解“负面”的现象。
有理数:分配的艺术

当我们学会把一个苹果分给两个人时,有理数就应运而生了。
有理数是可以表示为两个整数之比(即分数)的数,形式如下: a/b,其中 a, b ∈ ℤ, b ≠ 0
(我们没法把苹果分给“0”个人,所以分母不能为零,不然数学家真的会抓狂)。
- 除以 0 没有意义:如果分母为 0,无法找到任何数乘以 0 得到非零的结果,这样就会导致数学上的矛盾。
有理数,比如 1/3, 355/106, -2/3,甚至整数本身也是有理数,因为它们总是可以写成 n/1 的形式。
有理数的作用无处不在,但凡涉及“分配”或者“比例”,它们就会闪亮登场。
实数:无理数的加入
有理数家族已经够庞大了,但你以为这就是全部了?不不不,欢迎来到更广阔的实数世界!实数不仅包括有理数,还包括那些无法用分数表示的“神奇数”——无理数。

无理数的名字听起来有点“无理取闹”。要知道,古希腊毕达哥拉斯学派坚信,所有的事物都可以用整数或整数之比来表达:世界应当是整洁、有理且可以度量的。
不过其中一位成员希帕索斯在研究边长为 1 的等腰直角三角形的斜边长度时,发现结果竟然是 √2。他尝试用整数或分数来表达这个结果,可失败了——它无法用两个整数的比来表示,它的小数部分是无限不循环的,比如 √2 = 1.414213562373095...

就这样一直延续下去,还永远找不到重复的规律。
常见的无理数还包括:π(圆周率)、e(自然对数的底数)、φ(黄金分割比)、√3 等。
因此,实数包括了所有的有理数和无理数,形象地说,实数就是数轴上所有的点,从左到右,无穷无尽。

代数数 vs. 超越数:谁更高深?
接下来,会遇到了两个稍微抽象的概念:代数数和超越数。
代数数是那些能够成为某个整数系数多项式方程解的数。比如,3x² - 9x + 6 = 0 的解是 x = 1 和 x = 2,因此它们两个是代数数。
代数数不仅包括有理数,还包括一些无理数。比如,√2 就是方程 x² - 2 = 0 的解,φ 是方程 x² - x - 1 = 0 的解,所以它们也都是代数数的一员。
但并不是所有的数都能被整数系数多项式方程“驯服”。有些数,无论你如何组合整数系数的多项式,它们都不会成为解。这些数被称为超越数。
最著名的例子就是 π 和 e。无论你怎么组合整系数的多项式,它们就是不愿意成为方程的解。
复数:虚数和实数的完美结合
你以为故事就到这里结束了?不,欢迎来到 复数的世界。复数是由一个实数部分和一个虚数部分组成的,形式为 a + b,其中 是虚数单位,也是方程 x² + 1 = 0 的解—— 也是一个代数数。

虚数听起来有点像魔法,但它们非常实用,特别是在物理学、电力学和工程中有广泛的应用。通过复数,人们可以处理那些仅用实数无法解决的问题。
数的世界远不止于此
数的世界远不止这些,还有许多更高级的数系等待探索。
比如,四元数和 八元数扩展了复数,帮助人们处理三维和更高维的旋转问题;p 进数则在数论中扮演着重要角色,它通过质数的视角重新定义了“距离”,并为数论中的整除性和同余问题提供了强有力的工具。还有 超复数,如 双曲数和 双数,它们在物理和工程中有着特殊的应用,尤其是在处理时空几何和自动微分问题时。如果你认为无穷小只是微积分中的抽象概念,那么 超实数将颠覆你的想法,它们让无穷小和无穷大的操作变得严格且可行。
每一种数系都是理解世界的钥匙。而你我,正站在这条通向无限的道路上,保持好奇心,勇敢追寻!
(责任编辑:热门资讯)
-
 近日,有不法中介为达到营销目的,散播所谓“2024年征信恢复新规”不实言论,以此诱导社会公众。对此,中国人民银行征信中心发布声明称,目前并未有新规定发布,根据《征信业管理条例》第十六条规定,个人不
...[详细]
近日,有不法中介为达到营销目的,散播所谓“2024年征信恢复新规”不实言论,以此诱导社会公众。对此,中国人民银行征信中心发布声明称,目前并未有新规定发布,根据《征信业管理条例》第十六条规定,个人不
...[详细]
-
小米新车规划曝光:首款SUV明年发布,2026年推6座增程SUV
 IT之家 9 月 23 日消息,博世日前发布的技术路线图意外透露了小米汽车的产品规划。根据该路线图,小米计划在 2025 年发布两款新车型:小米 SU7 Ultra 和代号为 MX11 的首款 SUV
...[详细]
IT之家 9 月 23 日消息,博世日前发布的技术路线图意外透露了小米汽车的产品规划。根据该路线图,小米计划在 2025 年发布两款新车型:小米 SU7 Ultra 和代号为 MX11 的首款 SUV
...[详细]
-
 巴萨门将特尔施特根遭遇髌腱断裂的重伤,赛季报销。已退役的前巴萨门将布拉沃在接受采访时表示,如果巴萨打电话给他,他会做好准备。现年41岁的智利门将布拉沃在一个月前宣布退役,他曾在2014年至2016年效
...[详细]
巴萨门将特尔施特根遭遇髌腱断裂的重伤,赛季报销。已退役的前巴萨门将布拉沃在接受采访时表示,如果巴萨打电话给他,他会做好准备。现年41岁的智利门将布拉沃在一个月前宣布退役,他曾在2014年至2016年效
...[详细]
-
 作者|郑皓元钟雨润|实习生主编|陈俊宏在中秋之际,西凤酒因一场推广活动被卷入“风口浪尖”,因其旗下贴牌酒“国花瓷西凤酒”邀请了司马南作为嘉宾出席中秋活动引发大量负面舆论。今日,西凤酒方面向经销商、供应
...[详细]
作者|郑皓元钟雨润|实习生主编|陈俊宏在中秋之际,西凤酒因一场推广活动被卷入“风口浪尖”,因其旗下贴牌酒“国花瓷西凤酒”邀请了司马南作为嘉宾出席中秋活动引发大量负面舆论。今日,西凤酒方面向经销商、供应
...[详细]
-
 11月3日,中国证券报记者了解到,部分银行已开始受理存量房贷利率重定价周期调整申请。“11月1日上午,我在中国银行App上申请了重定价周期调整,由12个月调整至3个月,当天下午就收到变更申请已通过
...[详细]
11月3日,中国证券报记者了解到,部分银行已开始受理存量房贷利率重定价周期调整申请。“11月1日上午,我在中国银行App上申请了重定价周期调整,由12个月调整至3个月,当天下午就收到变更申请已通过
...[详细]
-
亚洲之光:大谷翔平53轰55盗再刷MLB历史纪录 有望冲60+60
 北京时间9月23日,MLB洛杉矶道奇6-5逆转险胜科罗拉多洛基,大谷翔平本场贡献1轰2盗率队取胜。大谷翔平本赛季数据继续提升至53轰55盗,继续刷新MLB历史纪录,且本赛季有望冲击60轰60盗神迹,无
...[详细]
北京时间9月23日,MLB洛杉矶道奇6-5逆转险胜科罗拉多洛基,大谷翔平本场贡献1轰2盗率队取胜。大谷翔平本赛季数据继续提升至53轰55盗,继续刷新MLB历史纪录,且本赛季有望冲击60轰60盗神迹,无
...[详细]
-
 19日晚间,ST盛屯公告,近日收到公司董事长张振鹏、总经理周贤锦、董事翁雄、董事会秘书邹亚鹏的书面辞职报告。根据《公司章程》的有关规定,辞职自辞职报告送达董事会之日起生效。就在9月13日,上海证券交易
...[详细]
19日晚间,ST盛屯公告,近日收到公司董事长张振鹏、总经理周贤锦、董事翁雄、董事会秘书邹亚鹏的书面辞职报告。根据《公司章程》的有关规定,辞职自辞职报告送达董事会之日起生效。就在9月13日,上海证券交易
...[详细]
-
 文|新熵 萧维当今年三月底,阿里临阵撤回菜鸟IPO时,肯定不会想到老对手丰巢的上市如此急迫。近日,顺丰旗下丰巢快递柜,正式向港交所递交IPO招股书,估值约250亿元人民币。作为国内快递配送"最后一公里
...[详细]
文|新熵 萧维当今年三月底,阿里临阵撤回菜鸟IPO时,肯定不会想到老对手丰巢的上市如此急迫。近日,顺丰旗下丰巢快递柜,正式向港交所递交IPO招股书,估值约250亿元人民币。作为国内快递配送"最后一公里
...[详细]
-
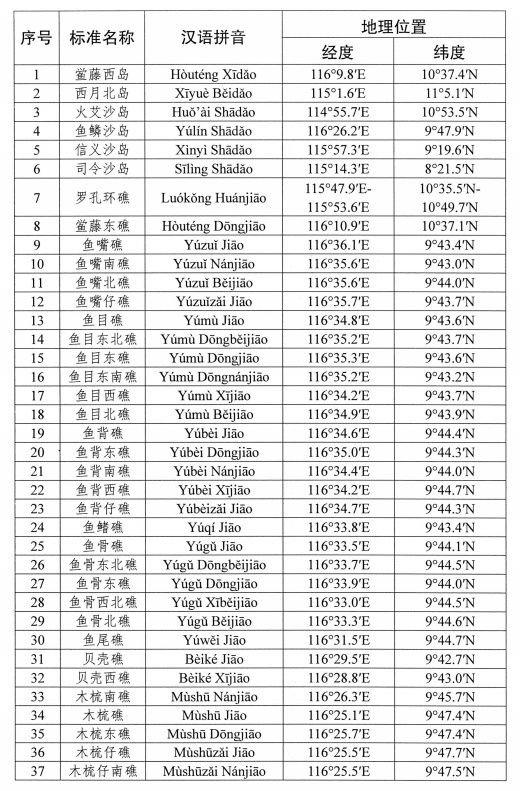 为进一步规范有关地名的使用,自然资源部、民政部公布我国南海部分岛礁标准名称。中国地名委员会1983年4月受权公布的《我国南海诸岛部分标准地名》和自然资源部、民政部2020年4月公布的《自然资源部
...[详细]
为进一步规范有关地名的使用,自然资源部、民政部公布我国南海部分岛礁标准名称。中国地名委员会1983年4月受权公布的《我国南海诸岛部分标准地名》和自然资源部、民政部2020年4月公布的《自然资源部
...[详细]
-
 据西班牙媒体Relevo最新报道,欧足联承认德西之战中库库雷利亚的手球存在误判。然而,有趣的是,欧足联在七月份还认为安东尼-泰勒对库库雷利亚的手球判罚无误。《图片报》在7月份报道表示,欧足联宣布安东尼
...[详细]
据西班牙媒体Relevo最新报道,欧足联承认德西之战中库库雷利亚的手球存在误判。然而,有趣的是,欧足联在七月份还认为安东尼-泰勒对库库雷利亚的手球判罚无误。《图片报》在7月份报道表示,欧足联宣布安东尼
...[详细]

 泽连斯基会见英摩法三国领导人 讨论对乌支持等问题
泽连斯基会见英摩法三国领导人 讨论对乌支持等问题 谷歌CEO皮查伊:AI不会取代程序员,反而会让更多人成为程序员
谷歌CEO皮查伊:AI不会取代程序员,反而会让更多人成为程序员 比亚迪A级SUV海狮05DM
比亚迪A级SUV海狮05DM 比亚迪第二代宋 Pro DM
比亚迪第二代宋 Pro DM 特朗普即将重返白宫,身上这些官司或将不了了之
特朗普即将重返白宫,身上这些官司或将不了了之
